迷路問題(一般形)

迷路問題とは

迷路問題はだいたい次のようなルールに基づいている。

• スタート(開始)地点とゴール(終了)地点がある。スタート地点を出発しゴール地点を目指す。
• 途中通る道が決まっている。途中原っぱを抜けていくというようなことはない。
• 同じ道は二度通ってはならない。
• 行き止まりとか障害物があって途中前へ進めなくなることがある。

迷路問題サンプル

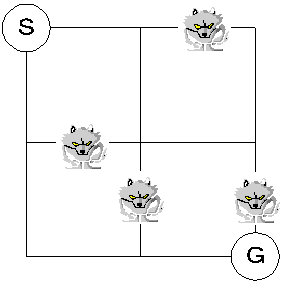
赤ずきんちゃんがおばあさんの家を目指す問題を考えてみる。START(S)からGOAL(G)まで狼(オオカミ)を避けて訪れるにはどのような経路を選択すれば良いでしょうか。

オオカミの絵はフリーのhttp://www6.ocn.ne.jp/~museum/animal/wolf/wolf.htmlの絵を利用させて貰いました。

この問題なら三歳位の知恵があれば簡単に解けるんじゃなかろうか。

では次のような問題だったらどうだろう。21枚の円形の紙がある。1地点を出発して21地点を目指す。途中数字が書いてある地点に到達すると紙をめくることが出来る。紙の裏にオオカミが書いてあるとそこを通過することが出来ない。オオカミ以外が書いてあれば通過することが出来る。どこにオオカミがいるかは事前に判らない。裏返した紙は元に戻さなければならない。

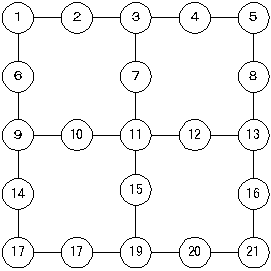
さてこうなると途端に大変になる。俯瞰(ふかん)で問題を眺めることが出来なくなるのである。コンピュータでプログラムを作成するということは俯瞰で物事を見ることが出来ない場合の対処方法と同じと考えて良い。

先が見えない状態で迷路を解く

オオカミがどこにいるか判らないので，どうやって先へ進むかルールを決めそれに従って行き先を決める。

• 道が分かれているところではどちらに進むか予め決めておく(例えば右,下,左,上の順)。
• 訪問してみてダメだと判ったら引き返す。
• 枝分かれしている全ての道がダメだったら更に引き返す。

このルールにのっとって上記問題を解いてみる。枝分かれのルールは，枝分かれしているところではまず右，下，左，上の順に訪問する。そのようにした場合の経路情報は以下の通り。

1. １⇒２⇒３⇒４×(オオカミ発見)→３
2. ３⇒７⇒１１⇒１２⇒１３⇒１６×(オオカミ発見)→１３
3. １３⇒８⇒５⇒４×(オオカミ発見)→５→８→１３→１２→１１
4. １１⇒１５×(オオカミ発見)→１１
5. １１⇒１０×(オオカミ発見)→１１→７→３→２→１
6. １⇒６⇒９⇒１０×(オオカミ発見)→９
7. ９⇒１４⇒１７⇒１８⇒１９⇒２０⇒２１(GOAL!)

⇒が先へ進むで，→は元に戻るときの記号とする。俯瞰(ふかん)できないと迷路問題は結構大変なことが判る。

コンピュータで迷路を解こうとすると

さて上記問題をコンピュータで解こうとするとどうなるだろうか。コンピュータで解こうとするとき問題になるのは以下のことである。

• 迷路をどうやって表現するか。
• 次に進む道をどうやって決定するか。
• オオカミがいる(障害がある)ことをどうやって表現(判断)するか。
• オオカミがいた(障害があった)ときどうやって戻るか。
• 「一度通った道を通らない」をどうやって実現するか。

一番肝心なのは迷路をどうやって表現するかということである。表現(データ構造)さえうまくできれば，後は何とかなる。

もっとも単純な迷路をコンピュータで解くことを考える

以下の迷路を考える。Ｓが開始地点，Ｇが終了地点とする。「こんなのは迷路じゃねー」と思う無かれ。こういうのをモデリングと言ってプログラムでは重要なアプローチである。

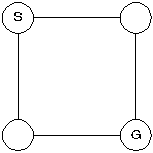
分かり易いように各地点に番号を振ってみる。

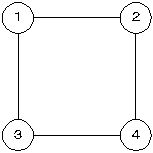
1がスタート地点，4がゴール地点，2,3が途中地点である。

どんなデータ構造にすれば良いか

この単純な迷路を言葉で表現してみる。

• スタート地点１
• ゴール地点４
• 途中２，３があります。

これだけだと実はダメである。

上の表現だと，以下のＡ〜Ｅのどれになるかが判らない。

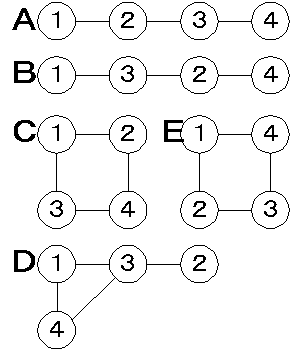
Ｃであることを明示するにはどうすれば良いか。

• スタート地点１
• ゴール地点４
• 途中２，３があります。
• １から２へ行けます。
• １から３へ行けます。
• ２から４へ行けます。
• ３から４へ行けます。

この条件を満たすのは上記Ｃのみであることが判る。

これをプログラムで表現するにはどうすれば良いか。

各地点に番号を振り，i地点からj地点へ到達可能である場合，P[i][j]=1, 到達出来ない場合P[i][j]=0 で表現する。

こうすることで上記迷路は以下のコードで表現できる。

int s=1;
int g=4;
int P[5][5];
P[1][2]=P[1][3]=P[2][4]=P[3][4]=1;

データはこれで表現できた。さてさてプログラムはどうすれば良いか。以下のような感じだろうか。

void findGoal( int p) // p地点からGOALまでの経路を探す
{
  if( p == g) {
    ゴールが見つかった
  }
  foreach next (p地点から到達可能な全ての地点)
    findGoal(next);
  }
}
void main()
{
  findGoal(s);
}

これを実際にプログラムして実行してみる。プログラムは以下の通り(肝になる部分を赤く表示した)。

#include <stdio.h>
#include <stdlib.h>

int s=1;
int g=4;
int P[5][5];

void findGoal( int p)
{
  if( p==g) {
    printf( "FindGoal\n");
    return;
  }
  for( int next=1; next<= 4; next++) { // pから到達可能な全ての地点を調べる
    if( !P[p][next]) {
      continue; // 到達出来ない地点は無視する
    }
    findGoal( next);
  }
}

int main( int argc, const char* argv[])
{
  P[1][2]=P[1][3]=P[2][4]=P[3][4]=1;
  findGoal( s);
  return 0;
}

実行結果は以下の通り。

FindGoal
FindGoal

経路情報を追加する

先の出力では，ゴールまで到達したみたいだが経路が不明である。経路情報を記録する必要がある。経路情報を記録するため以下のようにプログラムを改良する。

#include <stdio.h>
#include <stdlib.h>

int s=1;
int g=4;
int P[5][5];
int visit[10]; // 経路情報

void findGoal( int level, int p)
{
  visit[level] = p; // 経路を記憶
  if( p==g) {
    printf( "FindGoal\n");
    for( int i=0; i<= level; i++) { // 経路情報を出力
      printf( "%d ", visit[i]);
    }
    printf( "\n");
    return;
  }
  for( int next=1; next<= 4; next++) { // pから到達可能な全ての地点を調べる
    if( !P[p][next]) {
      continue; // 到達出来ない地点は無視する
    }
    findGoal( level+1, next);
  }
}

int main( int argc, const char* argv[])
{
  P[1][2]=P[1][3]=P[2][4]=P[3][4]=1;
  findGoal( 0, s);
  return 0;
}


これを実行すると以下の出力を得る。

FindGoal
1 2 4 
FindGoal
1 3 4 

正解。これで迷路プログラムは完璧か?

しかし，これでもまだ不十分である。実は今回の問題は以下のような迷路になっていた。

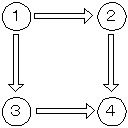
これを以下のように変更してプログラムを実行してみよう。双方向の矢印は互いに行き来できることを示す。

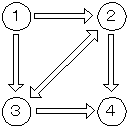
変更は以下のデータを追加することで可能。

P[2][3]=P[3][2]=1;

この修正を加えたプログラムを実行すると解を表示する前に以下のようなエラーを表示プログラムが異常終了してしまう。

何が悪いのか。findGoal()の先頭でデバッグ出力を入れて実行してみる。以下のような出力が得られる。

findGoal(level:1,p:1)
findGoal(level:2,p:2)
findGoal(level:3,p:3)
findGoal(level:4,p:2)
findGoal(level:5,p:3)
findGoal(level:6,p:2)
findGoal(level:7,p:3)
findGoal(level:8,p:2)
findGoal(level:9,p:3)

地点2と地点3を行ったり来たりしていることが判る。

一度通った道を二度通らない

一度通ったらその地点を記憶して，もう一度通ろうとしたら通れないようにする。プログラムは以下のようになる。

#include <stdio.h>
#include <stdlib.h>

int s=1;
int g=4;
int P[5][5];
int once[5]; // 1:一度通った, 0:まだ通っていない
int visit[10];

void findGoal( int level, int p)
{
  visit[level] = p;
  if( once[p]) return; // 一度通った地点
  if( p==g) {
    printf( "FindGoal\n");
    for( int i=0; i<= level; i++) {
      printf( "%d ", visit[i]);
    }
    printf( "\n");
    return;
  }
  once[p] = 1;
  for( int next=1; next<= 4; next++) { // pから到達可能な全ての地点を調べる
    if( !P[p][next]) {
      continue; // 到達出来ない地点は無視する
    }
    findGoal( level+1, next);
  }
  once[p] = 0;
}

int main( int argc, const char* argv[])
{
  P[1][2]=P[1][3]=P[2][4]=P[3][4]=P[2][3]=P[3][2]=1;
  findGoal( 0, s);
  return 0;
}

プログラムの実行結果は以下の通り。

FindGoal
1 2 3 4 
FindGoal
1 2 4 
FindGoal
1 3 2 4 
FindGoal
1 3 4

おー，完璧だ。

赤ずきんちゃんおばあさんの家を目指す

赤ずきんちゃんの問題に戻ろう。オオカミをどう表現するか?

オオカミがいると先へ進めない。と言うことは，単に「道がない」と考えれば良い。枝分かれ地点に番号を振ると以下の図になる。

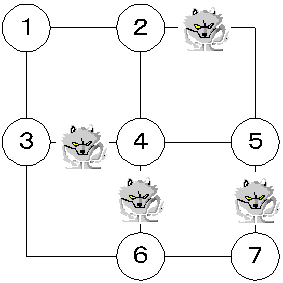
P[1][2]=P[2][4]=P[1][3]=P[3][6]=P[4][5]=P[6][7]=1

道は双方向なので反対側のデータも造る。

P[2][1]=P[4][2]=P[3][1]=P[6][3]=P[5][4]=P[7][6]=1

プログラムは以下の通り。

#include <stdio.h>
#include <stdlib.h>

int s=1;
int g=7;
int P[10][10];
int once[10];
int visit[10];

void findGoal( int level, int p)
{
  visit[level] = p;
  if( once[p]) return; // 一度通った地点
  if( p==g) {
    printf( "FindGoal\n");
    for( int i=0; i<= level; i++) {
      printf( "%d ", visit[i]);
    }
    printf( "\n");
    return;
  }
  once[p] = 1;
  for( int next=1; next<= 7; next++) { // pから到達可能な全ての地点を調べる
    if( !P[p][next]) {
      continue; // 到達出来ない地点は無視する
    }
    findGoal( level+1, next);
  }
  once[p] = 0;
}

int main( int argc, const char* argv[])
{
  P[1][2]=P[2][4]=P[1][3]=P[3][6]=P[4][5]=P[6][7]=1;
  P[2][1]=P[4][2]=P[3][1]=P[6][3]=P[5][4]=P[7][6]=1;
  findGoal( 0, s);
  return 0;
}

実行結果は以下の通り。

FindGoal
1 3 6 7 

数字を変更しても大丈夫なことを確認する。

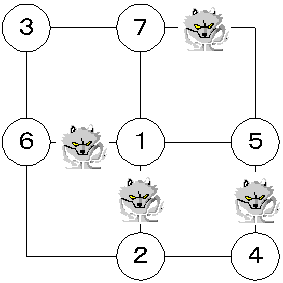
s=3
g=4
P[3][7]=P[3][6]=P[7][1]=P[1][5]=P[6][2]=P[2][4]=1
P[7][3]=P[6][3]=P[1][7]=P[5][1]=P[2][6]=P[4][2]=1

このときの出力は以下のようになる。

FindGoal
3 6 2 4 

条件付き迷路

A,B,Cの順に通って下さい。Xは通ってはいけません。

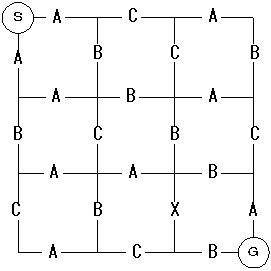
まずはデータをどうやって表現するか考える。以下のように番号を振って，番号間の移動をA:1, B:2, C:3 というように表現する。

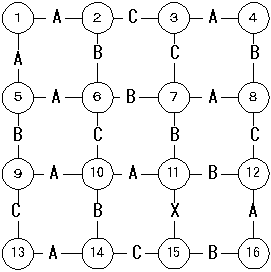
P[1][2]=P[3][4]=P[1][5]=P[5][6]=P[7][8]=P[9][10]=P[10][11]=P[12][16]=P[13][14]=1
P[2][6]=P[4][8]=P[6][7]=P[5][9]=P[7][11]=P[11][12]=P[10][14]=P[15][16]=2
P[2][3]=P[3][7]=P[6][10]=P[8][12]=P[9][13]=P[14][15]=3

反対側のデータは以下のようにプログラムの中で作る。

for( int i=0; i<= S; i++) for( int j=0; j<= S; j++) if( P[i][j]) P[j][i] = P[i][j];

プログラムは以下の通り。

#include <stdio.h>
#include <stdlib.h>

int s=1;
int g=16;
#define S 16
int P[S+1][S+1];
int once[S+1];
int visit[S+1];

void findGoal( int level, int p)
{
  visit[level] = p;
  if( once[p]) return; // 一度通った地点
  if( level > 1) {
    int prevType = P[visit[level-2]][visit[level-1]];
    int nowType = P[visit[level-1]][visit[level]];
    if( nowType == 1 && prevType != 3) return;
    if( nowType == 2 && prevType != 1) return;
    if( nowType == 3 && prevType != 2) return;
  }
  if( p==g) {
    printf( "FindGoal\n");
    for( int i=0; i<= level; i++) {
      printf( "%d ", visit[i]);
    }
    printf( "\n");
    return;
  }
  once[p] = 1;
  for( int next=1; next<= S; next++) { // pから到達可能な全ての地点を調べる
    if( !P[p][next]) {
      continue; // 到達出来ない地点は無視する
    }
    findGoal( level+1, next);
  }
  once[p] = 0;
}

int main( int argc, const char* argv[])
{
  P[1][2]=P[3][4]=P[1][5]=P[5][6]=P[7][8]=P[9][10]=P[10][11]=P[12][16]=P[13][14]=1;
  P[2][6]=P[4][8]=P[6][7]=P[5][9]=P[7][11]=P[11][12]=P[10][14]=P[15][16]=2;
  P[2][3]=P[3][7]=P[6][10]=P[8][12]=P[9][13]=P[14][15]=3;
  for( int i=0; i<= S; i++) for( int j=0; j<= S; j++) if( P[i][j]) P[j][i] = P[i][j];
  findGoal( 0, s);
  return 0;
}

プログラムの実行結果は以下の通り。

FindGoal
1 2 6 10 11 7 3 4 8 12 16

絵と見比べてみると正しいことが判る。